Even the most accurate predictions about patient response is ultimately of minimal value without a way to translate those predictions into "actionable items". In the world of radiation oncology, actionable is usually interpreted as RT treatment plans, i.e., the amount of dose delivered to each volumetric pixel (voxel), defined as the smallest (hypothetical) unit of the underlying tissue. This is the role of optimization, more specifically, adaptive optimization using the information provided by the predictive models. However, there are several concerns which have to be addressed: First, the optimization models are large-scale and highly nonlinear, and in some cases even nonconvex. Second, there are a number of uncertainty sources involved in not only the optimization model's parameters themselves, but in the predictions provided by the predictive models. Third, these predictions have to be considered over time, i.e., the problem is dynamic. Therefore, in order to fully arrive at an optimal or near-optimal solution for the problem, all three issues have to be efficiently tackled.
We use advanced optimization-based algorithms for updating the treatment plans based on incoming information. These include advanced methods in exact and approximate convex optimizations, conic optimization, and dynamic optimization. In addition, addressing the data and modeling uncertainties involved in the previous steps (biomarker discovery and predictive modeling) is handled via novel or state-of-the-art robust and partially-observable Markov decision processes (POMDP) algorithms to derive (near)optimal solutions which are robust against such uncertainties.
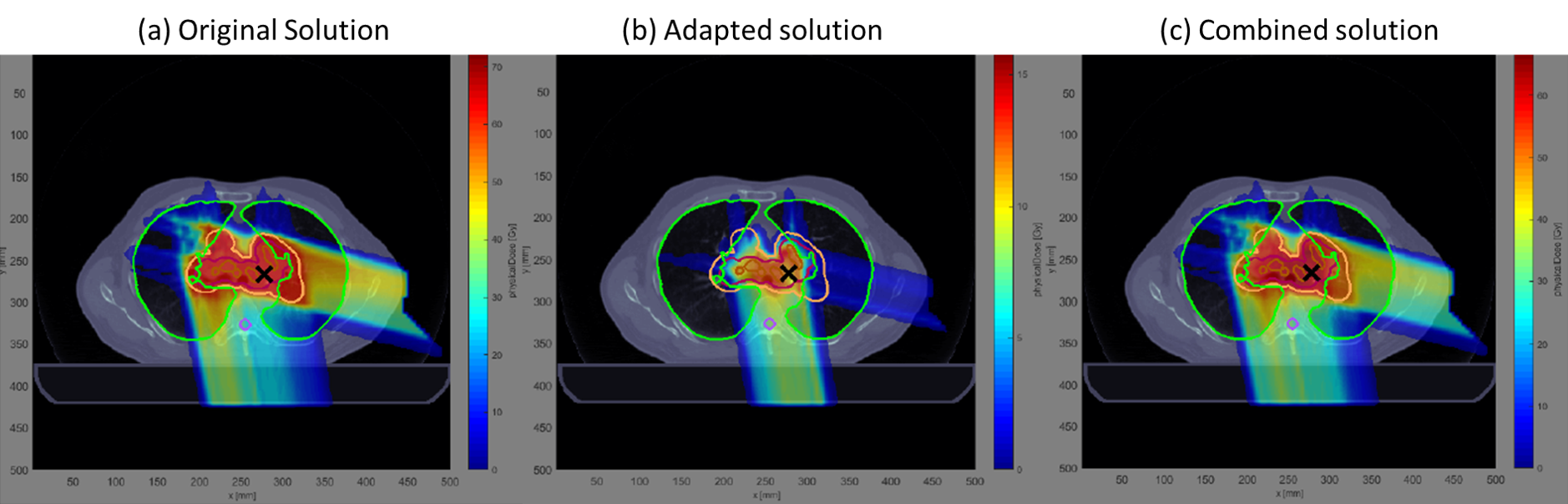
Example 1: Adjustable robust optimization to account for dynamic biomarker uncertainty
Any biomarker measurement contains certain amount of uncertainty due to, for instance, inherent noise or measurement errors. In order to properly account for such uncertainty when adapting the treatment plans based on them, one has to perform robust optimization. However, there is an element of time associated with biomarkers which are collected during the treatment time, that is, the true (noisy) value of the biomarkers are not known a priori, but has to be learned during the treatment course. We devised novel Adjustable Robust Optimization (ARO) techniques to account for this temporal uncertainty and deriving optimal robust solutions. Specifically, we present a mathematical framework that optimally adapts the treatment-length of an RT plan based on the acquired mid-treatment biomarker information, and also consider the inexact nature of this information. We formulate the adaptive treatment-length optimization problem as a 2-stage problem, where after the 1st stage we acquire information about model parameters and decisions in stage 2 may depend on this information.
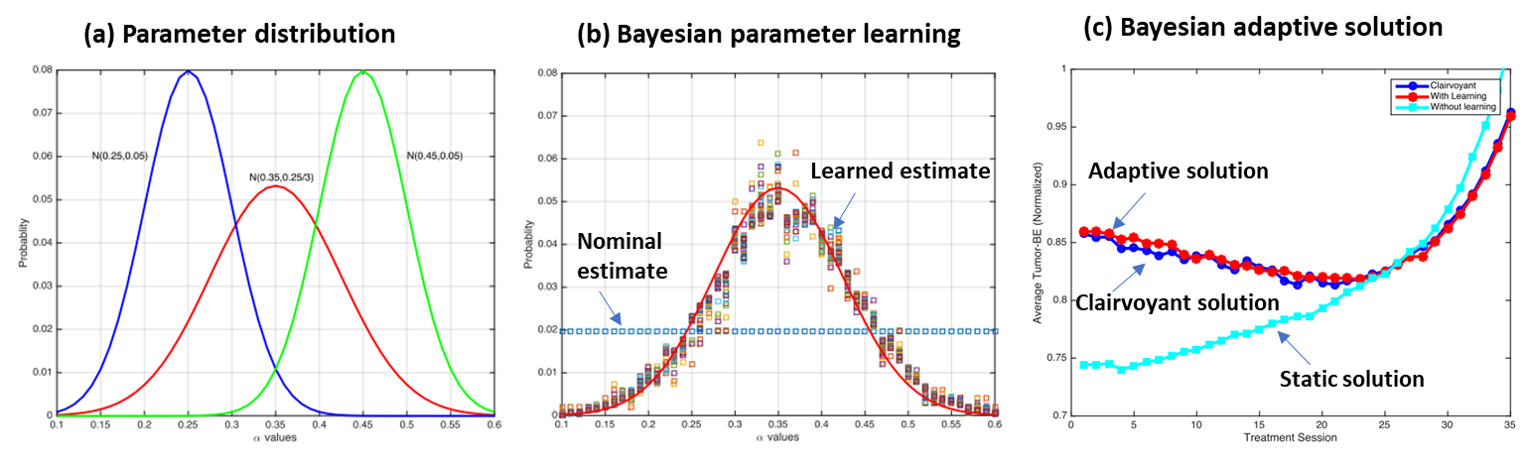
Example 2: Adaptive Bayesian learning to account for uncertainties in tumor's response parameter
In radiotherapy, one of the most important parameters in the popular linear-quadratic (LQ) model (which relates radiation dose to tumor response), is the tumor's response parameter α. However, the true value of this parameter is not readily known and can significantly differ across patient-population. However, it is now becoming more feasible to estimate this parameter for any given patient using molecular imaging or other types of biomarkers. However, one again has to deal with the fact that such information is only revealed partially (it contains noise) and gradually (over multiple treatment sessions) during the treatment. In this work, we have formulated and solved this problem using a dynamic optimization technique within a Bayesian framework. Each time new biomarker information becomes available, the algorithm updates the estimate for α using a Dirichlet prior and a Bayesian learning updating scheme. The problem is then solved to (near) optimality using state-of-the-art interior point method baked into a certainty equivalent control (CEC) framework.
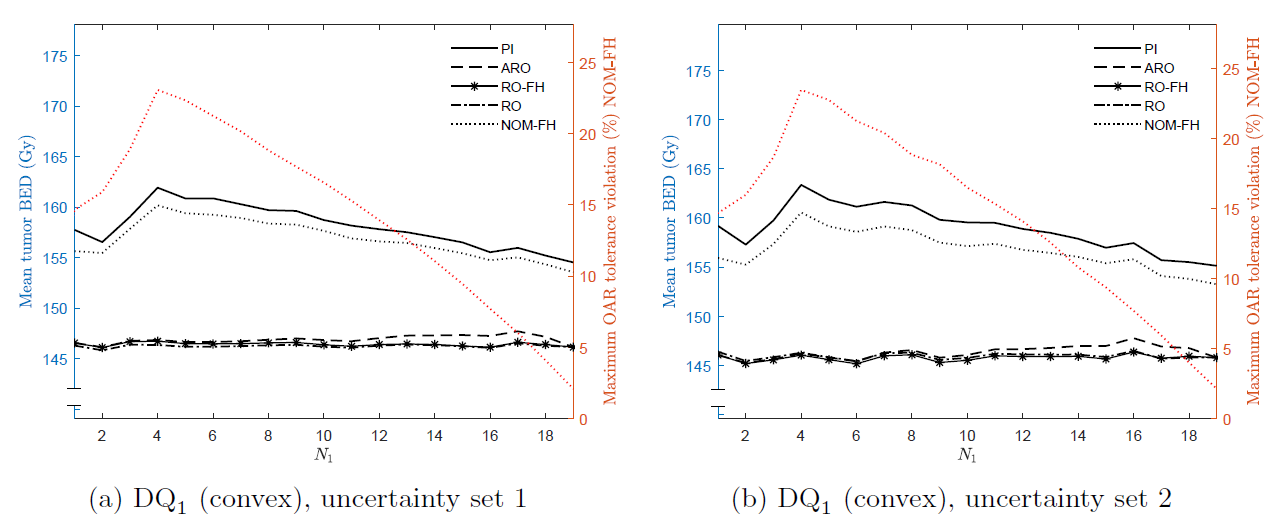
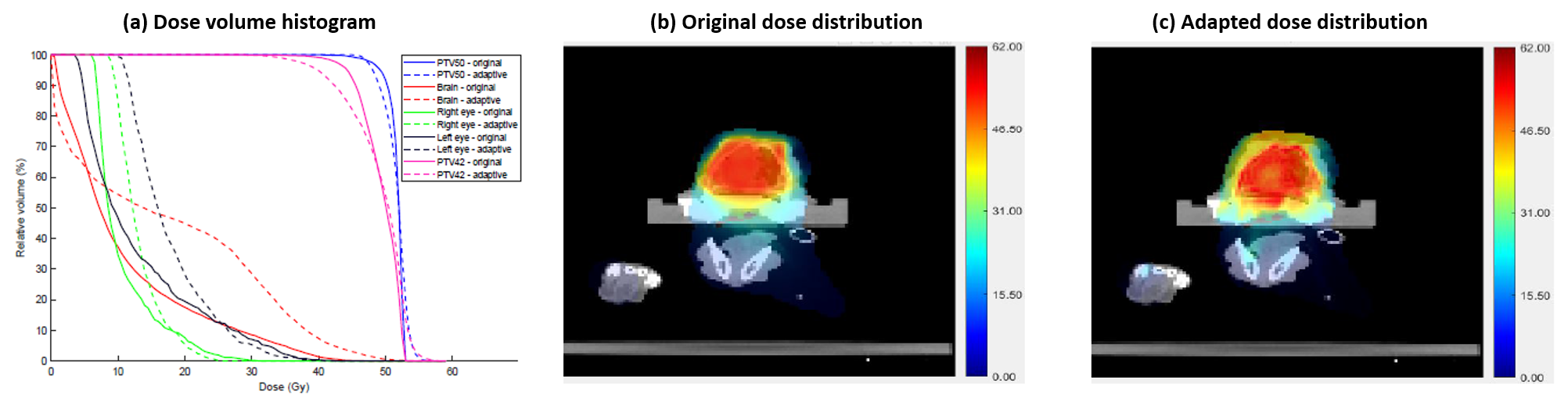
Example 3: Adaptive and robust treatment optimization using incoming imaging biomarker information
Today, many different types of candidate biomarkers have been proposed in the form of imaging and blood-based markers (see the "Biomarker Discovery" section). However, so far there has not been a systematic framework for adapting the treatment course according to these biomarker information. The goal of such an adaptation is to selectively increase the radiation dose for more radioresistant patients (without exceeding the tolerable threshold for toxicity), and de-escalate the dose for those who are deemed more responsive to treatment (i.e., more radiosensitive). In this work, we provide such a framework and introduce two different methods for adapting the treatment based on mid-treatment imaging biomarker information. We also address the uncertainty in the biomarker and derive robust solutions against such uncertainties. We base our methodology on a canine head-and-neck dataset for whom mid-treatment FLT PET images (a biomarker of tumor cell proliferation and activity) are available. The FLT images are used to estimate the "true" values for tumor α parameters.
Ongoing and Future Research
Our ongoing and future research in this area of personalized RT is focused on three main topics:
I. Devising efficient optimization algorithms for solving the large-scale biologically-driven problems, using advanced techniques rooted in Conic optimization, Pareto Robust Optimization (PRO), and Pareto Adjustable Robust Optimization (PARO) (with S. Eikelder, D. den Hertog).
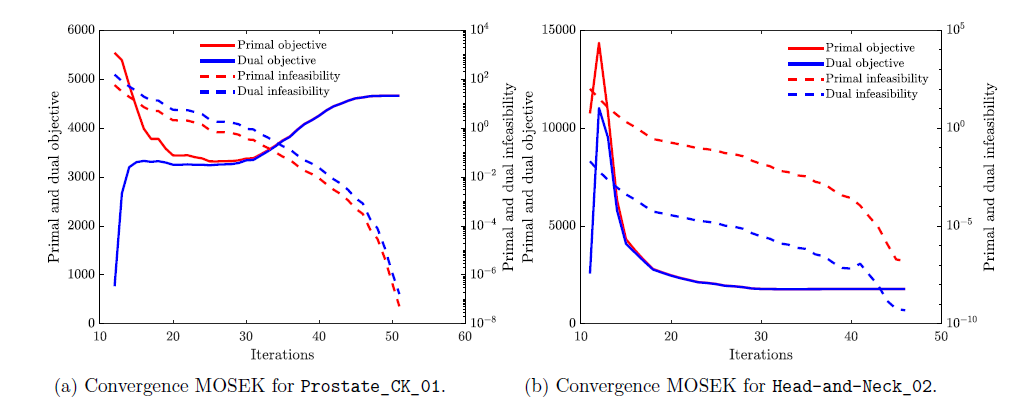
II. Direct incorporation of machine learning-based risk predictions into the treatment planning optimization using Simulation Optimization (SO) methods (with D. Maragno and D. den Hertog (U. Amsterdam).
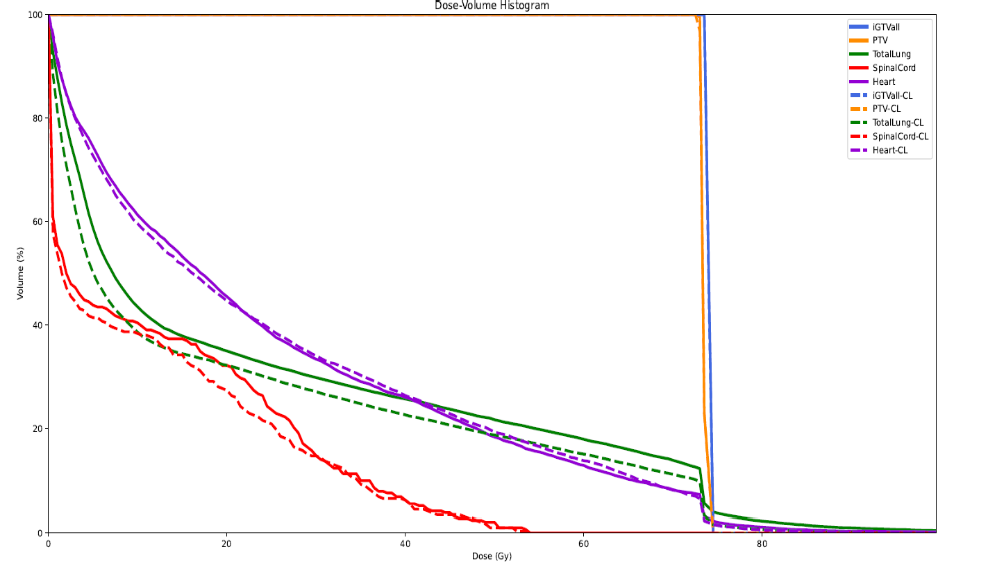
III. Dynamic and stochastic optimization algorithms for simultaneously addressing temporal and uncertain components of the model, using techniques in Optimal Stopping, (Partially-observable) Markov Decision Processed (MDP), and Reinforcement Learning(RL).
Interested in Collaborations?
We are continuously looking for interested collaborators and curious students to brainstorm, start new collaborations, and exchange knowledge. IF you are interested in one of the above-mentioned areas, please send us an email at
Selected Publications:
