(Jan Unkelbach, Ben Martin, Timothy Chan, and Thomas Bortfeld )
Introduction
The accuracy of intensity modulated proton therapy (IMPT) is potentially compromised by setup errors and uncertainties concerning the range of a proton beam in the patient. Uncertainties in the range may originate from artifacts in the CT image or the conversion of Hounsfield units to stopping powers. Another source of uncertainties are changes in the patient's geometry.
In classical radiotherapy with high energy x-rays, uncertainties due to motion and patient positioning can be accounted for by margins. In IMPT however, the concept of planning target volumes (PTVs) is principally flawed. This is, amongst other things, because one of the underlying assumptions behind the PTV concept is violated: the static dose cloud approximation (the dose distribution in space does not change due to patient motion) is invalid in proton therapy. Therefore, we work on robust and probabilistic optimization methods to directly account for uncertainties in the formulation of the IMPT treatment plan optimization problem.
Below we give an introduction to robust optimization methods in IMPT and illustrate results for a paraspinal tumor. Details of this work can be found in a number of publications: In [1] we introduce two concepts for handling range uncertainty (a probabilistic formulation and a worst-case approach) and demonstrate results for a stylized phantom. In [2] the probabilistic framework is extended to setup errors and we discuss results for a clinical paraspinal tumor. In [3] we compare range and setup errors to dose calculation errors and point out interrelations between both types of errors. Similar results have been obtained independently by Pflugfelder et al in [4].
Sensitivity of conventional IMPT plans
We consider the paraspinal patient shown in figure 1. The CTV deliniated in red entirely surrounds the spinal cord which is to be spared. The patient's CT features artifacts due to metal implants, leading to potential range errors. Three beams (at -45, 0 and 45 degrees) were used to optimize an IMPT plan for 3D spot scanning.
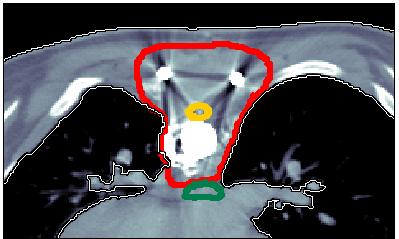
(Figure 1)
Figure 2 shows an IMPT treatment plan that was optimized without accounting for any type of uncertainty. Figure 2a shows the cumulative dose of all three beams for the nominal range and the nominal setup position. If no error occurs, a very homogeneous dose distribution can be delivered to the CTV and a good sparing of the spinal cord can be achieved. If we perform a sensitivity analysis of the plan, we observe that the dose distribution in figure 2a is highly degraded. Figure 2b shows the resulting dose distribution for an overshoot of 5 mm in water equivalant range (i.e. the bragg peak positions of all beamlets are shifted further into the patient). This sensitivity can be explained by analysing the dose contributions of individual beam directions (shown in figures 2d - 2f). The optimization assigns a high weight to bragg peaks placed in front of the spinal cord. This allows for the best dose sparing of the critical structure as the steep distal fall-off of the bragg peak is utilized. As a consequence, a very high dose is delivered to the spinal cord if the range of a pencil beam is larger than expected. Generally, dose gradients in beam direction make the plan very sensitive to range variations.
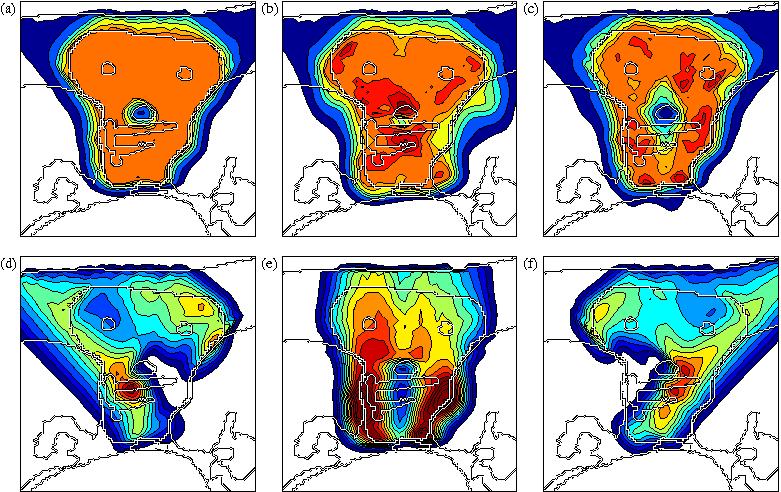
(Figure 2)
Figure 2c illustrates that the treatment plan is also sensitive to setup errors. It shows the resulting dose distribution for a 3.5 mm setup error posteriorly. The rigid shift of the patient has no impact on the dose deliverd by the beam at 0 degrees. However, the oblique beams at -45 and 45 degrees hit the patient surface at a different position. Their dose contributions are shifted relative to each other and consequently do not add up to a homogeneous dose distribution in the CTV. In this case, the oblique beams are shifted apart and cause cold spots around the spinal cord.
Although this section analyses a treatment plan that does not apply a margin to the CTV, it is evident that the PTV concept cannot solve the problem sufficiently. A PTV margin around the CTV could only reduce the underdosage of the CTV at the boundary due to geometric shifts of the dose distribution. It cannot account for dose inhomogeneity in the CTV and overdosage of the spinal cord due to misalignements of beams and density heterogeneities. Defining a PTV has no influence on the occurance of steep dose gradients (within the dose distribution of a single beam) inside the CTV, as would be necessary to improve the robustness of a treatment plan. In addition, the dose distribution around the spinal cord cannot be controlled by a PTV approach since a margin extension of the CTV at the transition to the spinal cord would simply eliminate the structure to be spared.
Methods to incorporate range uncertainties in IMPT optimization
We apply concepts that are known as robust optimization and stochastic programming in the optimization community. These methods have in common that the dose delivered to the patient depends on a set of uncertain parameters. For a rigid systematic setup error, this could be a 3-dimensional vector describing the patient shift. For range errors this could be a vector of range shifts for every pencil beam.
In the probabilistic treatment planning approach, a probability distribution is assigned to the vector of uncertain parameters which reflects the probability that a given error scenario occurs. Treatment planning is performed by optimizing the expected value of an objective function, where the expectation is taken over all possible errors that may occur, weighted with their probability.
In a robust planning approach, the uncertain parameters are assumed to vary within some interval (uncertainty set). Treatment planning can be performed by optimizing the worst case treatment that can occur for any error in the uncertainty set.
Results of probabilistic treatment plan optimization
The sensitivity of IMPT treatment plans against errors can be greatly reduced using probabilistic or robust optimization methods. Figure 3 shows the treatment plan obtained by accounting for a Gaussian setup error of 2.5 mm standard deviation in all directions and a Gaussian range uncertainty of 5 mm standard deviation for all pencil beams. Figures 3a shows the dose distribution for the nominal case (no setup or range error occurs). Figures 3b and 3c show the dose distributions for a 5 mm range overshoot and a 3.5 mm setup error posteriorly. Despite the error, the dose in the tumor remains widely homogeneous and the sparing of the spinal cord is preserved. Figures 3d-3f show the dose contributions of the three beams for the nominal case, which explains how robustness of the plan is achieved. Protection against range uncertainty is achieved by avoiding steep dose gradients in beam direction in the dose contributions of individual beams. This includes avoiding the placement of the distal edge of a bragg peak directly in front of the spinal cord. Robustness against setup errors is achieved by reducing dose gradients in left-right direction.
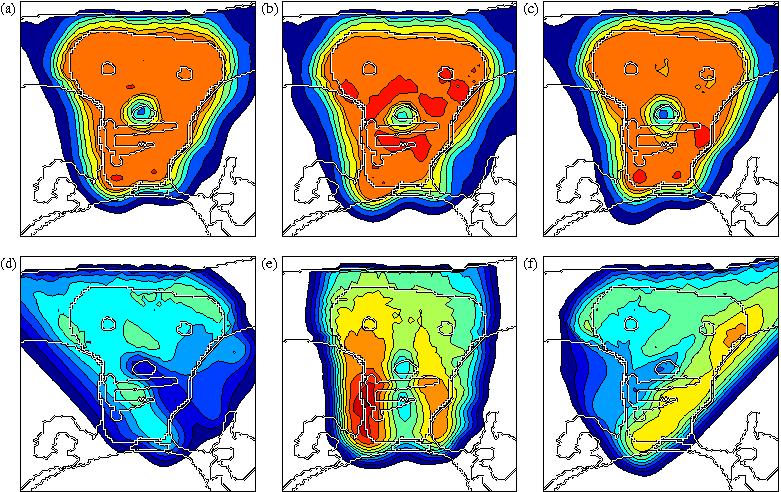
(Figure 3)
References
- J. Unkelbach and T. C. Y. Chan and T. Bortfeld. Accounting for range uncertainties in the optimization of intensity modulated proton therapy. Phys. Med. Biol., 52, p2755-73. 2007
- J. Unkelbach, B. Martin, M. Soukup and T. Bortfeld. Reducing the sensitivity of IMPT treatment plans to setup errors and range uncertainties via probabilistic treatment planning. Medical Physics, 36(1), p149-163. 2009
- J. Unkelbach, M. Soukup, M. Alber, and T. Bortfeld. Range, Setup and Dose Calculation Errors in IMPT and their Interrelation. Proceedings of the World Congress on Med. Phys. and Biomed. Engineering. Vol 1, p900-903. 2009
- D. Pflugfelder, J. Wilkens, and U. Oelfke. Worst case optimization: a method to account for uncertainty in the optimization of intensity modulated proton therapy. Phys. Med. Biol., 53, p1689-1700, 2008.
