Overview
For several years our group, along with our collaborators ITWM and RaySearch Laboratories, has been advancing the field of multi-criteria optimization (MCO) radiotherapy planning. The basic planning challenge of radiotherapy is to handle the tradeoff between getting the required dose to the tumorous regions and not overdosing the surrounding healthy organs. An MCO approach to treatment planning allows the treatment planners and physicians to explore and understand these tradeoffs thus providing a means to select the best plan for each patient.
Our approach to MCO treatment planning is based on the computation of a set of Pareto optimal plans. These are treatment plans that cannot be improved in any one objective without worsening another objective. The set of all Pareto optimal plans constitutes the Pareto surface, and this is the fundamental object which we aim to compute and present in a useful way.
Exploration of the Pareto surface as a means of treatment planning should allow for the selection of better plans, and do so much more quickly than current treatment planning methods. With standard (i.e. non-MCO) systems, there are often many iterations between the treatment planner and the TPS, and between the treatment planner and the physician. This can easily add up to hours and days to plan a single case, and it is our hypothesis that with a multi-criteria system, this planning time can be drastically reduced. We are in the process of testing this hypothesis using the prototype system from RaySearch Laboratories, and the initial data looks very promising: physicians are able to select a plan using the Pareto surface navigation interface within 5 minutes, and the Pareto surface computation itself is template-based and takes only 10 minutes or so of planning time.
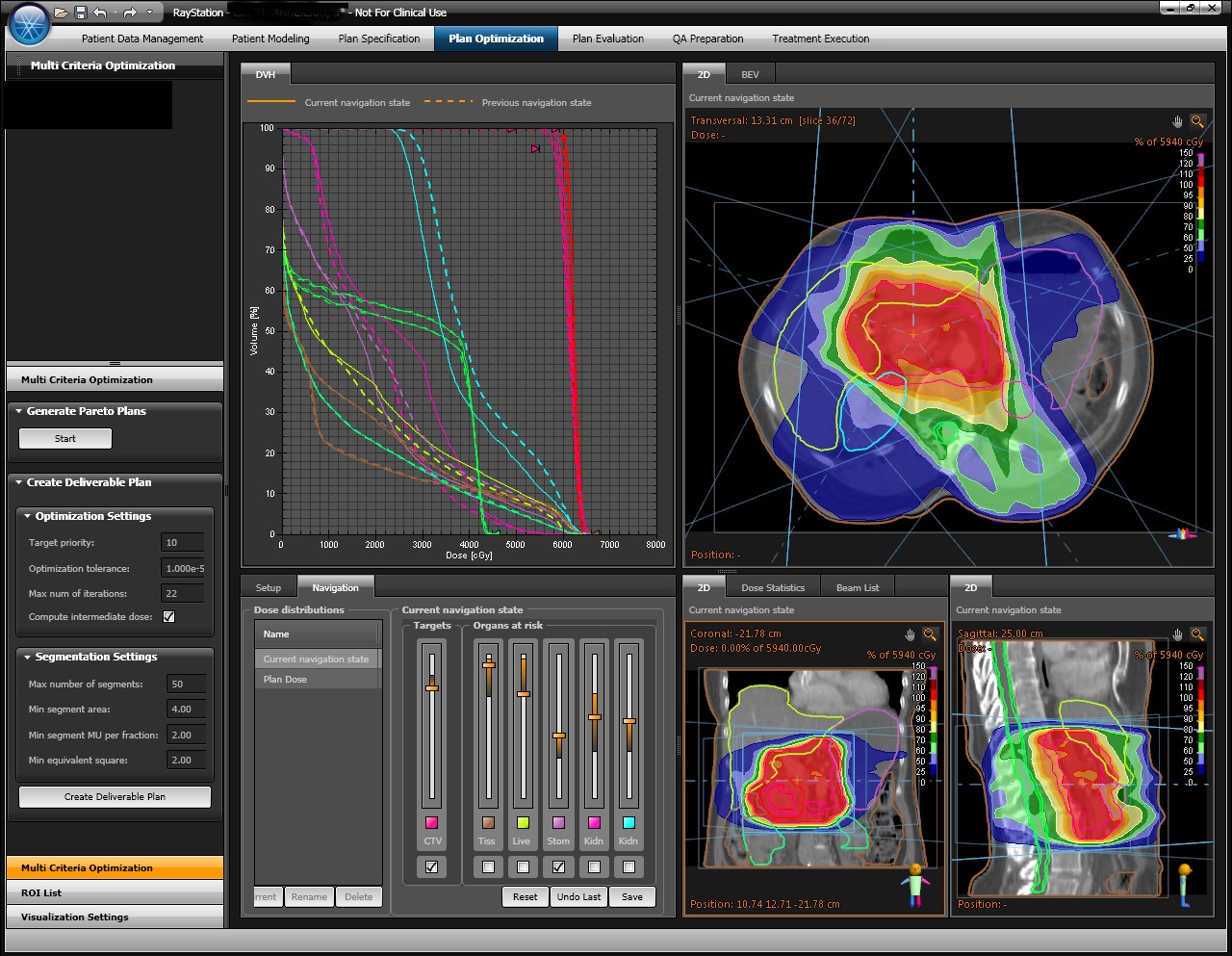
Screen shot of the treatment planning system from RaySearch, with the MCO module developed in collaboration with our team at MGH.
Some projects
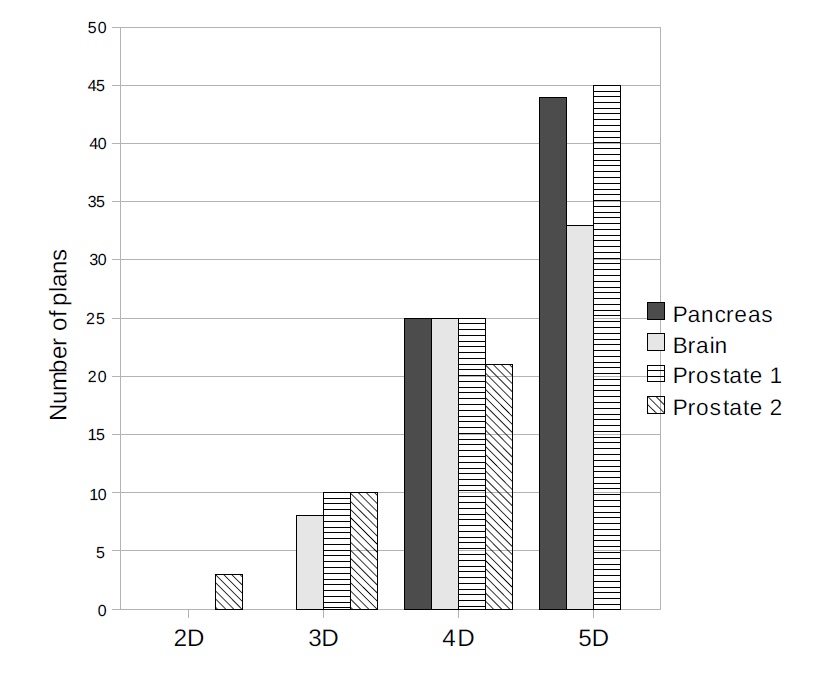
Number of plans necessary for an adequate representation of the Pareto surface
We approximate the Pareto surface by a discrete set of plans on the surface and their convex combinations. There are typically anywhere from 3 to 10 objectives in radiation therapy planning, and important questions are, how many Pareto optimal solutions need to be calculated in order to have an adequate representation of the Pareto surface, and how does this number depend on the number of objective functions used.
These questions can be addressed both mathematically and clinically. Thus far, we have addressed them mathematically. The easiest way to investigate the 'how many plans' issue is to sequentially generate points on the Pareto surface and check to see how new each point is, with regard to the already computed plans and their convex combinations. This was done here, which also used principal component analysis to examine Pareto databases, and looked into the idea of correlated objective functions.
We have also looked into a non-linear version of PCA which is better suited to applying PCA to Pareto databases. This shows that the true dimension of Pareto surfaces is much smaller than the number of objectives used, and is usually no larger than 4. Such analyses support the idea that the number of plans needed for a radiotherapy Pareto database is modest.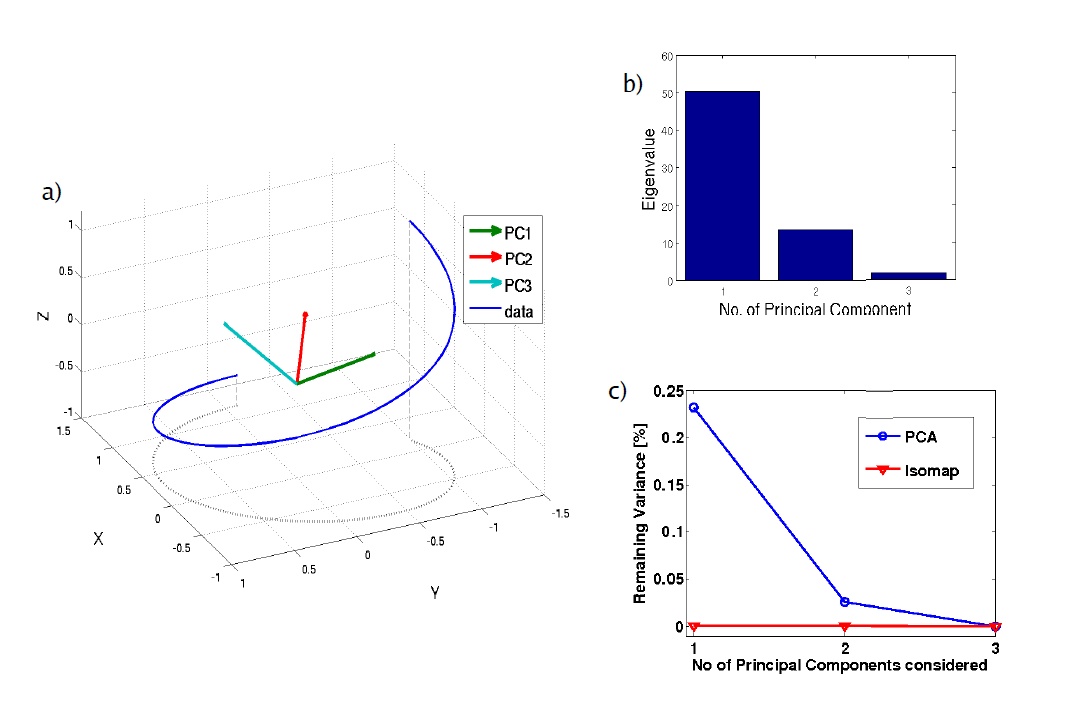
The isomap method finds lower dimensional representations of data but does not assume the data are scattered in a Gaussian ellipsoid, as is the assumption for principle component analysis (PCA). For example, if data are along a spiral in 3D, as in the figure above, the isomap method can detect that the data are actually one-dimensional, whereas PCA would not do a good job reducing the dimensionality of these data.
More rigorous analysis of the number of plans needed questions can be found here, and this is related to the nice new algorithm (an improvement on the PGEN algorithm) by G. Rennen which is found here.
Number of plans necessary to represent various clinical Pareto surfaces to within a 5% accuracy. Accuracy in this case means that all Pareto optimal solutions are at most 5% away from the approximated Pareto surface, in each objective value.
Fast optimization and MCO database creation for IMPT
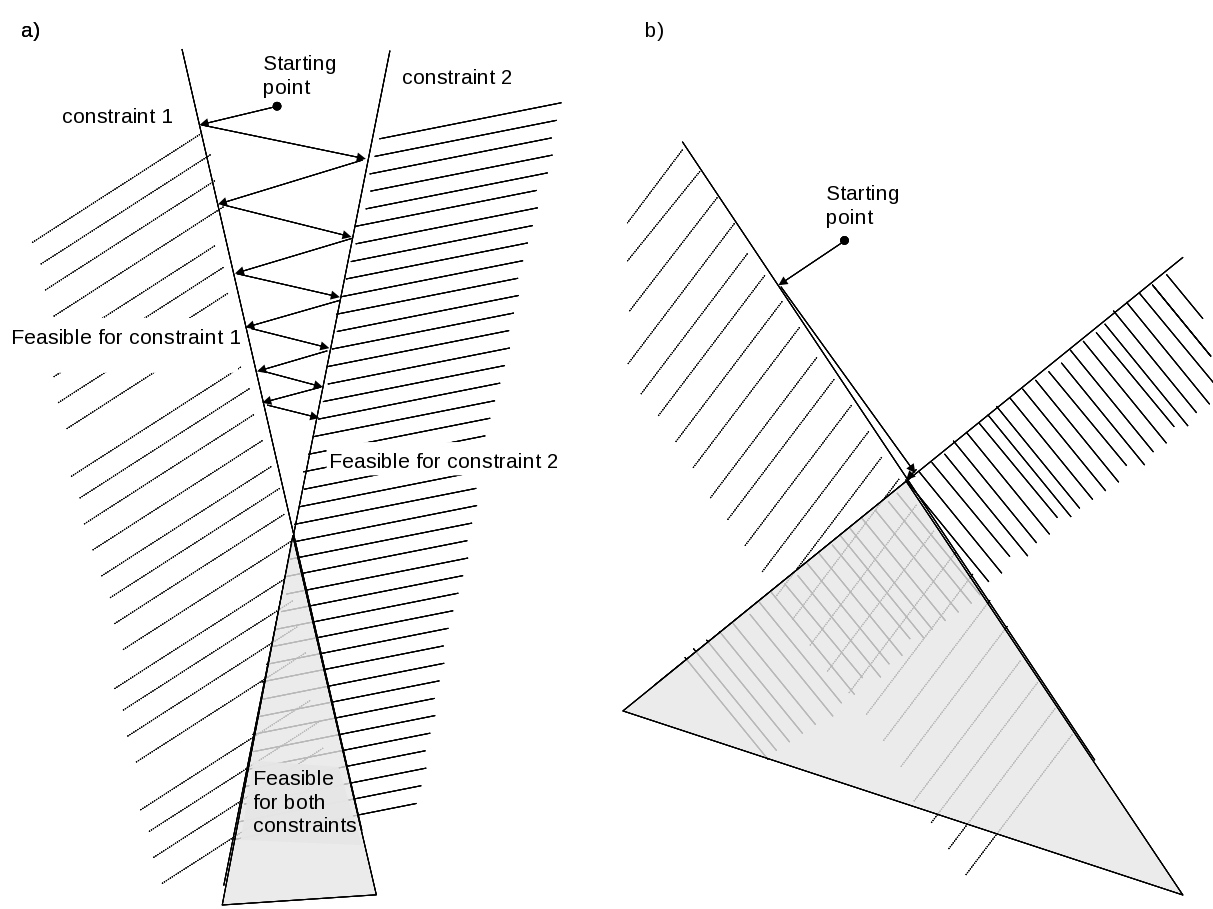
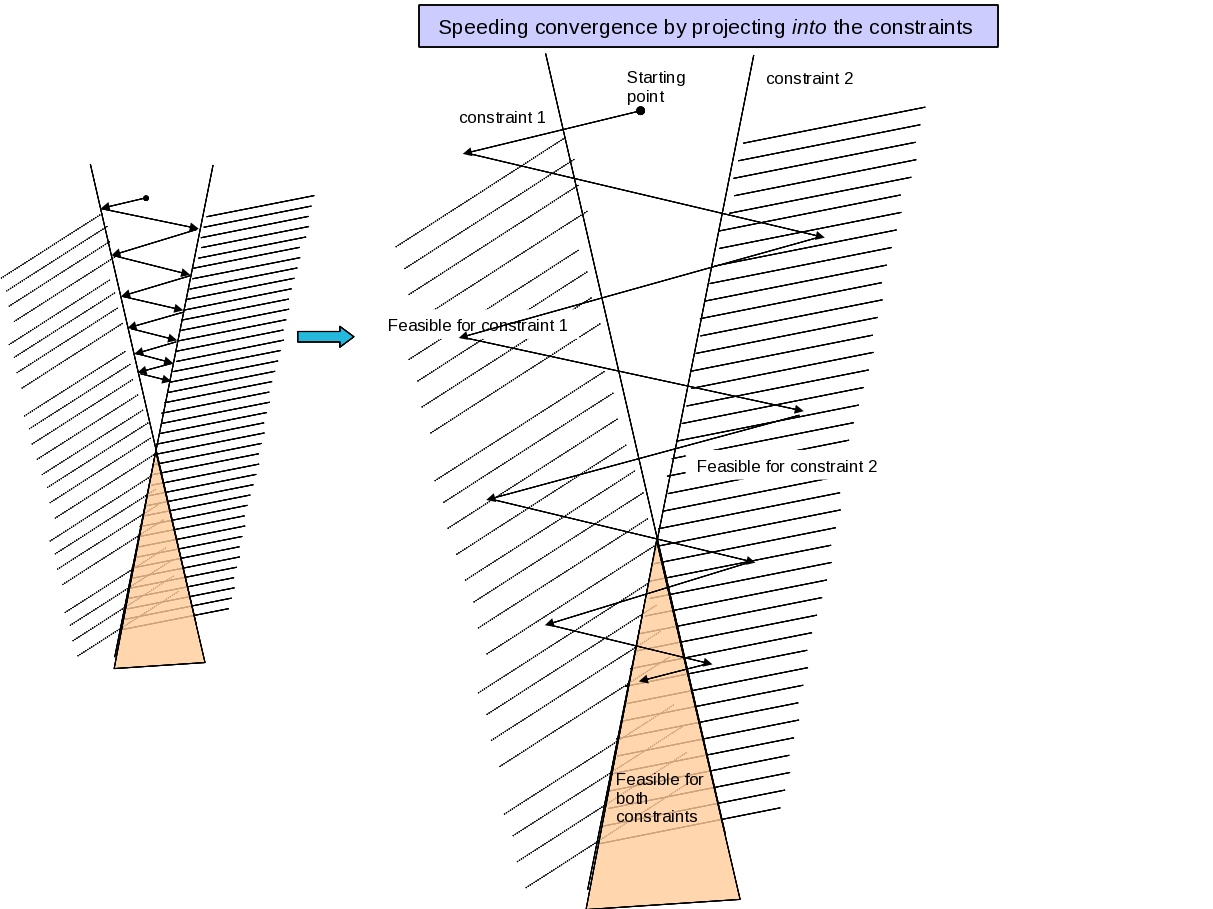
We have developed a customized convex solver to speed up the database generation process for intensity modulated proton therapy (IMPT). The basic idea is to turn an optimization problem into a feasibility problem (the objective function becomes a constraint that we iterate on to find its optimal value). Projection onto convex sets (POCS - which is called ART3+O, refer to figures below) turns out to be a very fast strategy for IMPT, as well as IMRT, since most of the voxel-level constraints are effectively independent due to small beamlet size and the physical large distance between most voxels. Also, projecting beyond the constraint boundary speeds the convergence up greatly. See the figures below. Details can be found in this pre-print.
 |
|
This figure displays how projection methods converge faster when the underlying constraints are orthogonal to each other. |
 |
|
Projection methods can also be improved by projecting into feasible region for a constraint, rather than just onto it. |
The result is that our POCS based solver is orders of magnitude faster and more memory efficient than commercial convex solvers applied to the radiotherapy problem, and this results in very fast database generation. Instead of the database generation process happening overnight, it happens in 5 to 10 minutes.
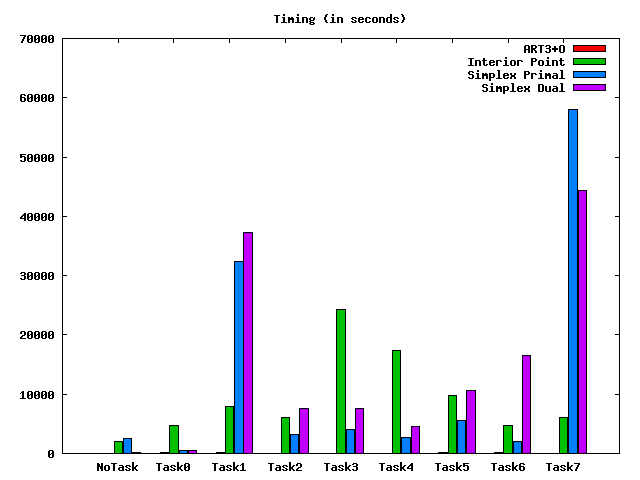
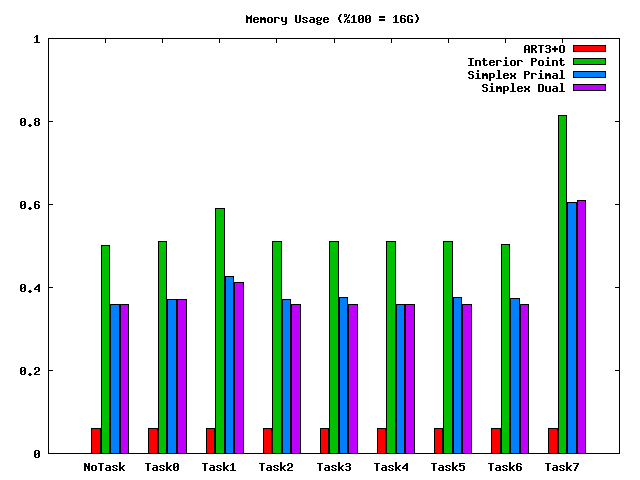
The tasks refer to different database plans. We see that for each task, the ART3+O is dramatically faster than the general purpose linear solvers implemented in Mosek (which is a great product, it is just not customized to our problem!). The ART3+O projection algorithm also has almost no memory overhead: it works directly with the Dij matrix
Advances in Pareto surface navigation
Multiple psurfs
The number of options available in radiotherapy is growing at a fast rate. Today, a radiotherapy patient might see 3D-conformal therapy, IMRT, protons, VMAT, or some other modality. In order to extend the Pareto surface MCO approach to the modality decision, we are investigating the exploration of multiple Pareto surfaces at the same time. A simple method has been devised to navigate a set of surfaces, and is explained in the paper Simultaneous navigation of multiple Pareto surfaces, with an application to multicriteria IMRT planning with multiple beam angle configurations.
2Dnav
We are developing a new navigation algorithm that is based on viewing a 2D tradeoff surface selected from the underlying higher dimensional Pareto surface. One benefit of this approach, described here, is that the user can visualize the tradeoff surface, and this might lead to better insight during navigation.
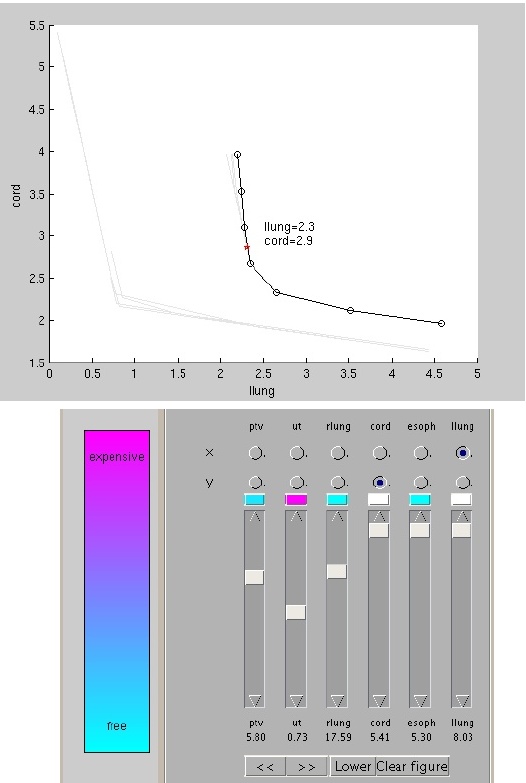
Prototype 2D navigation system. Sliders are constraints the user imposes during navigation, and radio buttons are used to select which two objectives to view the tradeoff between. The colors above the sliders display the effect that moving that slider will have on the currently viewed 2D Pareto surface: cyan means the curve will not be affected by a slight change in the slider level, pink means a large change will occur.
Directly deliverable navigation
IMRT delivery happens using a multi-leaf collimator (MLC), and a standard optimization procedure is to first optimize beamlet weights and then as a second step convert those weights into MLC segments for delivery. The current MCO system by RaySearch, under evaluation at MGH and Herlev Hospital in Denmark, requires a final step to do this conversion, which can alter the plan after navigation. Directly deliverable navigation refers to a navigation system where what you see is what you get, but this is much harder mathematically.
Understanding plan quality versus treatment delivery time
The simplest radiotherapy plan – an open field from one direction – takes the smallest time to deliver, but it is also not in general good in terms of dose distribution. On the other hand, a highly complex plan, requiring lots of entrance angles and lots of MLC blocking (that is, intensity modulation) at each angle, is superior dosimetrically, but this comes at the cost of prolonged treatment time. With the current push towards VMAT (rotational arc therapy, available on Elekta and Varian linacs), which promises high quality plans in much faster delivery time, it is even more pressing to understand the tradeoff between plan quality and treatment delivery time. Our first paper on this included the number of monitor units into the MCO Pareto surface calculation and showed that one can usually dramatically reduce the number of MU without degrading the plan quality.
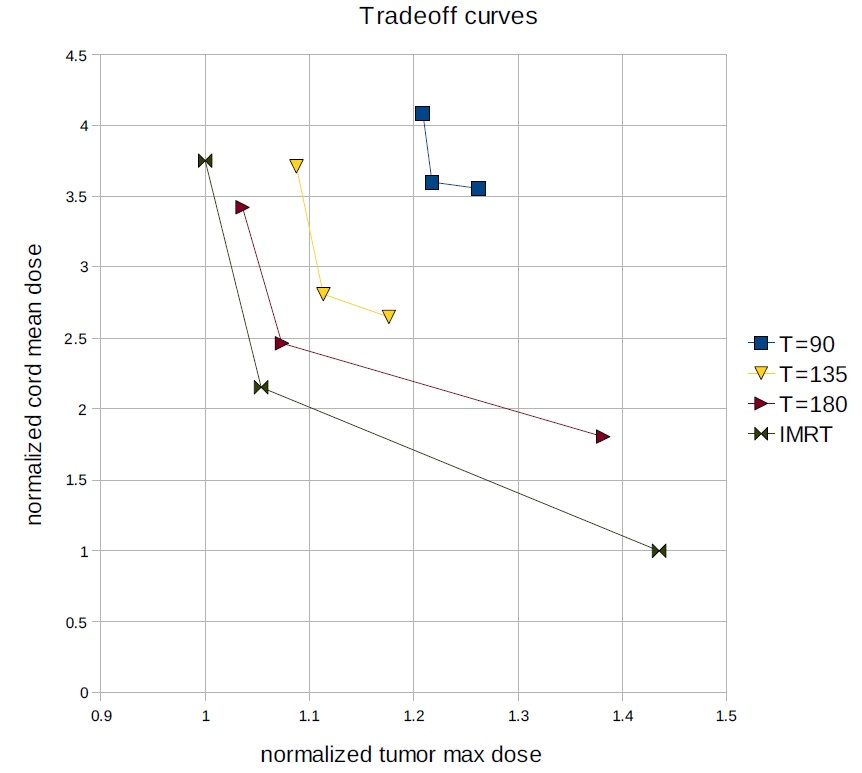
Another theoretical work, available here, models the gantry and MLC in a simplified 2D setting, and is based on letting the optimizer come up with the best plan – whether it be IMRT or VMAT or something in between – given a dosimetric objective function and a maximum beam-on-time. This analysis points out that if beam-on-time is allowed to be very high, the optimizer will shoot from a few select IMRT angles instead of a VMAT arc. On the other hand, if beam-on-time is highly constrained, then a VMAT solution is optimal. For practical cases, this work shows that a good planning strategy, for VMAT or IMRT, is to solve an IMRT optimization problem for many possible beam angles (for example, a beam every 4 degrees) and let the optimizer automatically choose which angles are best for that case.
T=90 is equivalent to one VMAT rotation at constant (maximum) speed, and T=180 is enough time for 2 rotations. In this phantom 2D case, the cord is near the target and to spare it well necessitates a carving out of the dose distrbution. This complex dose distribution therefore requires more time to achieve, and the dosimetric tradeoff curves are notable worse for T=90. The "IMRT" curve is obtained byallowing full intensity modulationat all of the angles modeled (every 4 degrees) and thus serves as a lower bound on the achievable Pareto curves.
Additional Publications