(Timothy Chan, Ben Martin, and Thomas Bortfeld)
Overview
This research is focused on the management of uncertainty in the radiotherapy planning process. For example, how does one account for the movement of a lung tumor during treatment as the patient breathes? How does the filling and emptying of the bladder affect the day to day location of a prostate tumor? These are the types of questions we try to address, and our method of choice is robust optimization.
Robust optimization is a relatively new and 'hot' topic in the optimization community. The basic premise is that by reformulating the original problem, or by solving a sequence of problems, we may find a solution which is robust to the uncertainty in the data. So, given uncertainty in say, the location of the tumor, we try to engineer treatment plans which will guarantee that the tumor receives no less than 95% of the prescribed dose, for example.
One of the earliest papers on robust optimization, by Soyster [1], considered simple perturbations in the data and aimed to find a reformulation of the original problem such that the resulting solution would be feasible under all possible perturbations. Subsequent, ground-breaking work by Ben-Tal and Nemirovski [2,3], El-Ghaoui et al. [4,5], and Bertsimas and Sim [6,7], extended the framework of robust optimization, and included sophisticated solution techniques with non-trivial uncertainty sets describing the data.
One avenue of research being undertaken at MGH involves taking the formulation of the uncertain inverse planning problem, and reformulating it to a mathematically equivalent, but deterministic problem. Then, one just needs to solve this new problem which is similiar to the "nominal" inverse planning problem to arrive at a "robust" treatment plan.
Another area of research includes the analysis of tumor position data, either through a surrogate marker, or through internal fluoroscopic data. Such analyses will help us craft more reliable models of data uncertainty, and will subsequently allow us to improve our treatment plans.
Clinical applications: lung motion in IMRT planning
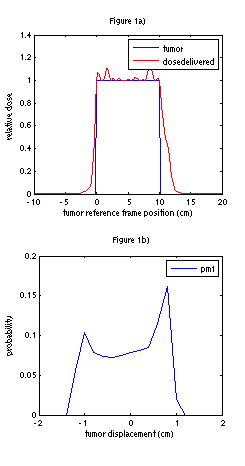
By applying ideas from robust optimization, we can generate treatment plans which are robust to intra-fraction motion such as breathing. The next two figures illustrate the possible negative effects of taking uncertainty for granted. Figures 1 and 2 show that if the patient breathes differently from what is planned or expected, and the treatment plan does not take into account this possible uncertainty, then the same plan can result in two very different dose distributions.
Figure 1a) shows the resulting dose distribution if an IMRT plan is optimized using the probability mass function (pmf) in Figure 1b), and the realized pmf is exactly the same as the one used for planning.
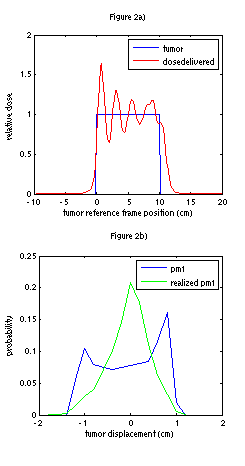
Figure 2a) shows the resulting dose distribution from the same plan if the patient now breathes according to the green pmf in Figure 2b), and not the blue one as planned.
Clearly the dose distribution in Figure 2a) is very poor, and motivates the work on robust optimization as a way to mitigate uncertainty.
The next two figures show the usefulness of the robust methodology in the inverse planning regime. This particular methodology uses "error bars" on the probability mass functions to account for uncertainty. The basic idea is to protect against uncertainty in the variation of the pmf, as long as the variations remain within the error bars. If one prefers more conservative solutions, the error bars could be made larger. On the other hand, if a patient exhibits almost machine-like breathing, then small error bars can be used to create less conservative plans.

Figure 3a) shows the dose distribution arising from a robust IMRT plan, using the blue pmf in Figure 3b) for planning, with the red error bars. Note that the dose distribution shown is for a realized pmf which is exactly the same as the one that was used in the planning.

Figure 4a) shows the dose distribution resulting from the same robust plan using the same planning pmf, but now, the realized breathing pmf is the green one.
Comparing Figure 3a) and Figure 4a), we see that the resulting dose distributions are quite similar, even though the realized pmf is dramatically different from the planned pmf in Figure 4.
Overall, we can see that the dose distribution for the robust treatment plans remains consistent even though the probability distributions describing the tumor locations are quite different.
Collaborators
Yair Censor (University of Haifa, Israel)
John Tsitsiklis (MIT)
Operations Research Center (MIT)
References
- Soyster, A. L. Convex programming with set-inclusive constraints and applications to inexact linear programming, Oper. Res., 21, 1154-1157. 1973.
- Ben-Tal, A. and Nemirovski, A. Robust solutions of Linear Programming problems contaminated with uncertain data, Math. Program., 88, 411-424. 2000.
- Ben-Tal, A. and Nemirovski, A. Robust solutions to uncertain programs, Oper. Res. Letters, 25, 1-13. 1999.
- Ben-Tal, A. and Nemirovski, A. Robust convex optimization, Math. Oper. Res., 23, 769-805. 2000.
- El-Ghaoui, L. and Lebret, H. Robust solutions to least-square problems to uncertain data matrices, SIAM J. Matrix Anal. Appl., 18, 1035-1064. 1997.
- El-Ghaoui, L., Oustry, F., and Lebret, H. Robust solutions to uncertain semidefinite programs, SIAM J. Optim., 9, 33-52. 1998
- Bertsimas, D. and Sim, M. The Price of Robustness, Oper. Res., 52, 35-53. 2004
- Bertsimas, D. and Sim, M. Robust Discrete optimization and Network Flows, Math. Prog. B, 98, 49-71. 2003.
