Motivation
Glioblastoma differ from many solid tumors in the sense that they grow infiltratively. Instead of forming a solid tumor mass with a defined boundary, glioblastoma are characterized by a smooth gradient of the tumor cell density. It is well known that tumor cells infiltrate the adjacent brain tissue and can be found several centimeters beyond the enhancing tumor mass that is visible on MRI.
In current clinical practive, radiotherapy planning is based on the gross tumor volume (GTV) visible on MRI. Many practitioners account for the infiltrative growth by expanding the GTV with a 1-3 centimeter margin to form the clinical target volume (CTV), which is irradiated to a homogeneous dose of 60 Gy. Target delineation can potentially be improved by accounting the anisotropic spatial growth patterns of gliomas, which are observed in histopathology and MR imaging:
- Anatomical boundaries: The dura, including its extensions falx cerebri and tentorium cerebelli, represents a boundary for migrating tumor cells. Also, except for rare cases of CSF seeding, gliomas do not infiltrate the ventricles.
- Tumor cells infiltrate gray matter much less than white matter.
- Tumor cells seem to migrate primarily along white matter fiber tracts.
Approach
Accounting for these growth characteristics requires an interdisciplinary effort involving mathematical modeling techniques, image processing, and analysis of clinical data. We investigate the use of a phenomenological tumor growth model for treatment planning, which replicates these growth patterns. The model is based on the Fisher-Kolmogorov equation, a partial differential equation of reaction-diffusion type. The model predicts the spatial distribution of tumor cells in regions of the brain that appear normal using current imaging techniques. It is personalized for a given patient using MRI data obtained routinely for glioma patients. More specifically, a segmentation of the brain into white matter, gray metter, cerebrospinal fluid, and tumor. The brain tissue segmentation allows us the solve the model equations on the patient specific geometry. The target volume for radiotherapy planning can be defined as an isoline of the simulated tumor cell density.
Illustration
In preliminary studies we have identified situations in which the use of the tumor growth model for radiotherapy target definition leads to differences compared to the clinical plan that was actually delivered. This is illustrated in the figures below:
Figure 1 shows the T1 post contrast image of a GBM located in the left parietal lobe, close to the falx and the corpus callosum. Figure 4 shows the FLAIR image of the same patient, revealing peritumoral edema surrounding the central tumor mass. Figure 2 shows the segmentation of the brain into white matter, gray matter and CSF as well as the segmentation of the tumor into enhancing core (blue) and peritumoral edema (red).
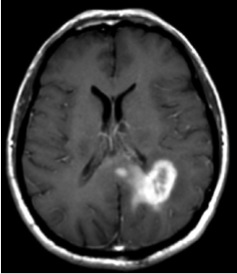Figure 1 
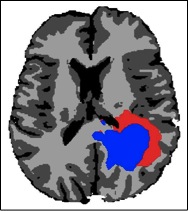Figure 2
Figure 3 shows the simulated tumor cell density using the growth model. The model reproduces important spatial growth patterns of glioblastomas: The falx is modeled as an anatomical boundary, which prevents tumor cells from migrating into the contralateral hemisphere. In addition, the corpus callosum, white matter fiber tracts connecting the cerebral hemispheres, is modeled. The corpus callosum provides a route for contralateral spread of tumor cells, which is replicated by the model. Furthermore, the glioma growth model allows us to describe reduced infiltration of gray matter surrounding major sulci, which can be seen primarily in the region of the lateral sulcus.
Figure 3 
Figure 4
Figure 4 illustrates the use of the growth model for target delineation. It compares the manually delineated target (yellow) used in the clinical treatment plan to the target contour derived from the model (red). The red contour corresponds to an isoline of the tumor cell density that encloses the same total volume as the manually defined target. For this patient, the model suggests a further extension of the target into the contralateral hemisphere.
